I recently learnt a really neat trick when it comes to proving two quantities are equivalent. It started of with my supervisor claiming that for some ![]() and
and ![]() ,
,
(1) ![]()
is obvious. To me, it was not obvious at all, and may not be so obvious to you either. But what my supervisor was referring to was a trick that saves a lot of time when it comes to analysis, and so today, I will be talking about it.
I will first prove 1 before I show you the trick. We firstly need to understand the notation in 1;
![]()
is called a \textit{multi index} and it is used to raise vectors to powers. For some
![]()
The degree of ![]() is
is ![]()
With this in hand, we can re-write 1 as
(2) ![]()
Now, for the equivalence symbol; ![]() means we can find two constants
means we can find two constants ![]() and
and ![]() such that
such that
![]()
and we say that
We shall first prove that there exists a constant ![]() such that
such that
![]()
To do this, we take a small subset of the multi-indices that satisfy ![]() , the index
, the index ![]() which has zero in every entry and also the indices
which has zero in every entry and also the indices ![]() for which
for which
(3) ![]()
We call the set of these indices ![]() and we note that
and we note that
(4) 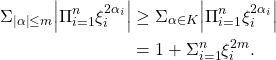
So taking ![]() , we have proved the first direction. Now, we wish to prove that there exists a constant
, we have proved the first direction. Now, we wish to prove that there exists a constant ![]() such that
such that
![]()
Prepare yourself for trick number 1 that will make your life so much easier, because the left hand side is just a finite sum, we only need to control the term ![]() by
by ![]() . Then we can take
. Then we can take ![]() where
where ![]() is the number of elements in the set
is the number of elements in the set ![]() and the result will follow.
and the result will follow.
We will assume without loss of generality, that ![]() is an increasing sequence. We begin by applying the Cauchy-Schwartz inequality:
is an increasing sequence. We begin by applying the Cauchy-Schwartz inequality:
(5) 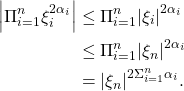
We have two cases, if ![]() then we have that
then we have that
(6) ![]()
and the result follows for this case.
However, if ![]() then knowing that
then knowing that ![]() we can write
we can write
(7) ![]()
and the result follows.
So we have proved that
(8) ![]()
but there is an intuitive way to look at this problem.
Firstly, consider the finite sum for ![]()
(9) ![]()
If ![]() , we can control the sum by
, we can control the sum by ![]() but if
but if ![]() we can control it by
we can control it by ![]() , and so in general,
, and so in general,
(10) ![]()
What we did was look at extreme cases and saw how all the other cases in between them could be controlled, if we controlled the extreme ones. This is the trick! Now let’s apply it to 2 which is
![]()
Again, we note that we only need to control the term that is being summed, and not the entire sum, as we saw from the proof. We now look at the extreme cases, if ![]() is the index with zero in every entry, then
is the index with zero in every entry, then
![]()
and if ![]() we can control these cases by
we can control these cases by
![]()
since ![]() for all
for all ![]() . Hence, by an intuitive path, we have arrived at 2.
. Hence, by an intuitive path, we have arrived at 2.
We note that in this trick, we only care about the order of these expressions, we look at the extreme cases of the order and note that we can control everything in between the extreme cases.
Stay tuned to the next blog post to see this trick, (and many more!!) in action.

Recent Comments