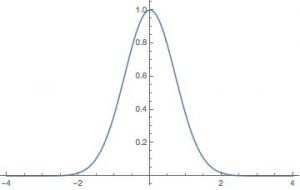
In quantum mechanics, we cannot speak of the exact location of a particle, but rather, we talk about the probability of a particle being in a certain region of space. Mathematically, we describe this using a probability density function, known as the wave function, where the area under the wave function gives the probability of finding it in that region of space. For example, consider the wave function shown below.
The particle is very likely to be in-between ![]() and
and ![]() , almost certainly in that region, but we cannot know exactly where it will be at any instant of time. So what happens when we try to take a measurement of it’s position? Well, in first year physics courses, we are taught that once we try to measure the position of a particle, the wave function collapses to a single point. By taking a measurement, you remove the uncertainty in the position and we know exactly where the particle is. Now although this may sound weird and hard to get your head around, this is beautifully shown in the mathematics behind this.
, almost certainly in that region, but we cannot know exactly where it will be at any instant of time. So what happens when we try to take a measurement of it’s position? Well, in first year physics courses, we are taught that once we try to measure the position of a particle, the wave function collapses to a single point. By taking a measurement, you remove the uncertainty in the position and we know exactly where the particle is. Now although this may sound weird and hard to get your head around, this is beautifully shown in the mathematics behind this.
These wave functions, let’s give them the name ![]() can be expressed as vectors that exist in Hilbert space (I’ll talk about this in a later post!). Now these vectors can be acted upon by things we call operators, functions that operate (do stuff) to our wave function. Now when we take a measurement of position, mathematically, this corresponds to acting on our wave function
can be expressed as vectors that exist in Hilbert space (I’ll talk about this in a later post!). Now these vectors can be acted upon by things we call operators, functions that operate (do stuff) to our wave function. Now when we take a measurement of position, mathematically, this corresponds to acting on our wave function ![]() with the position operator,
with the position operator, ![]() . This is represented as
. This is represented as
![]()
and this will give us the possible positions that our particle can be in. Now the position operator just corresponds to multiplying our wave function by the function ![]() . That is
. That is
![]()
These operators also satisfy what is called an eigenvalue equation,
![]()
where ![]() is a real number. Now what we hope to do is re-arrange this above equation (which represents us taking a measurement of position) and solve for the eigenvalues, which will in turn give us the possible positions of our particle.
is a real number. Now what we hope to do is re-arrange this above equation (which represents us taking a measurement of position) and solve for the eigenvalues, which will in turn give us the possible positions of our particle.
![]()
Now this is interesting! What this final line imply about our wave function ![]() (it is non-zero)? Well it means that:
(it is non-zero)? Well it means that:
![]()
![]()
Graphically it looks like this:
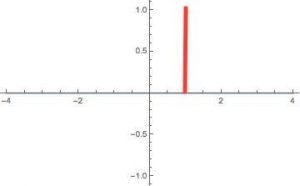 The wave function has collapsed to a single point! So this means that once you take a measurement of position, you know exactly where your particle is. There you go, the mathematics behind collapsing wave functions.
The wave function has collapsed to a single point! So this means that once you take a measurement of position, you know exactly where your particle is. There you go, the mathematics behind collapsing wave functions.

Trackbacks/Pingbacks