The Basis Theorem

Not going to go into too much detail about it, instead we will jump straight into the proof. But just so you know what your dealing with, the theorem says that if $p$ and $q$ are continuous on some interval $I$ then:

there are two linearly independent solutions ( 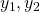$y_1,y_2$ ) to $L(y)=0$
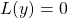
and that if 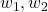$w_1,w_2$ are a pair of linear independent solutions to 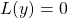$L(y)=0$ , any solution 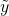$\tilde{y}$ is given by a linear combination of these two solutions, i.e.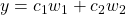 $y=c_1w_1+c_2w_2$

This second conclusion is what we want! (It is what we will use in solving these differential equations).

proof.

Proving the first statement caused me a bit of a headache, but I think taking some time to understand what we need to prove will ease things up.

In order to prove (1) we need to show that there exists two linearly independent solutions to

$L(y)=y''+py'+qy=0.$

Now since this equation is completely general, where $p$ and $q$ are assumed to be continuous, we just need to find 2 specific solutions for this general equation that are linearly independent, and we have proved that for any second order homogeneous equation, these 2 specific solutions will always work, and hence, we proved 1.

Let us start by picking an $x_0 \in I$ , where $I$ is the interval in which $p$ and $q$ are continuous. Now we will pick two solutions, $y_1$ and $y_2$ , where $y_1$ solves the initial value problem:

$L(y)=0, y(x_0)=1, y'(x_0)=0$

and $y_2$ solves:

$L(y)=0, y(x_0)=0, y'(x_0)=1$

Before we go into why we chose those, take a minute to check that by Fundamental Theorem of Existence and Uniqueness 3, that there actually exists a unique solution to the initial value problems above.

Okay so, to understand why we chose those initial conditions, we need to first know how we are going to check for linear independence. Because $y_1,y_2$ are solutions to the homogenous equation and $p,q$ are continuous, we can use the Wronskian Theorem! Now the Wronskian evaluated at a specific point is:

which has to be non-zero for $y_1,y_2$ to be linearly independent. So we need to pick values $y_1(x_0), y'_1(x_0), y_2(x_0), y'_2(x_0)$ , that will give a non-zero determinant. And using the chosen values from above, we get:

which is non-zero. So we have just shown that $y_1$ and $y_2$ are linearly independent.

As mentioned above, it doesn’t feel like we have proven anything. But what we have just shown is that for any second order linear homogeneous equation, the $y_1,y_2$ pair that we cooked up above, are two linearly independent solutions to it. Hence there will always be at least these two solutions to any second order homogeneous linear equation, which proves our first conclusion that:

there are two linearly independent solutions ( $y_1,y_2$ ) to $L(y)=0$

Now to prove (2), just a reminder of what we need to prove:

if $w_1,w_2$ are a pair of linearly independent solutions to $L(y)=0$ , any solution $\tilde{y}$ is given by a linear combination of these two solutions, i.e. $\tilde{y}=c_1w_1+c_2w_2$

Let us begin with what we have: $w_1,w_2$ are linearly independent solutions to $L(y)=0$ . From our Wronskian Theorem:

$W(w_1,w_2)(x_0) \neq 0.$

Now, a solution to the homogeneous equation $L(y)=0$ is $\tilde{y}.$

We don’t know what this is! In fact we are trying to prove that it is equal to

So for now (this is us getting fancy) let us form two equations with two unknowns $(c_1,c_2)$ as follows:

Where the second equation is just the derivative of the first and both are evaluated at some point $x_0$ . Why did we do this system in particular? We will answer this question at the end as it will make more sense, but for now, just trust me.

What we want to know is the following:

“Is our proposed solution $c_1w_1+c_2w_2$ the same as our actual solution $\tilde{y}$ ?”

To find this out, we first need to figure out whether we can find $c_1,c_2$ that solves our system above.

The determinant of the co-efficient matrix for this system is just $W(w_1,w_2)(x_0)$ (remember that $c_1,c_2$ are our unknowns here). And since $W(w_1,w_2)(x_0) \neq 0$ there exists a unique solution for $c_1,c_2$ .

But wait! That doesn’t prove that $\tilde{y}=c_1w_1+c_2w_2$ , all we have shown is that there exists $c_1,c_2$ that solve the system of equations above. In the part that follows, we show that they are equal.

To make what comes next easier to digest, let us define:

$z=c_1w_1+c_2w_2.$

Now both $\tilde{y}$ and $z$ are solutions to the IVP:

$L(y)=0, y(x_0)=\tilde{y}(x_0), y'(x_0)=\tilde{y}'(x_0)$

This is why we specifically chose the above system! It has hidden in it that $z$ satisfies the initial conditions to this IVP. More specifically the system says the following:

$z(x_0)=\tilde{y}(x_0), z'(x_0)=\tilde{y}'(x_0).$

So this is the big trick in this proof, choosing the right system of equations that allows to now compare two solutions to the same IVP, using the Fundamental Theorem 3. Very cool!

By the Fundamental Theorem 3, there is a unique solution to this IVP, and hence

$z=\tilde{y}.$

DONE!

Well, I hope that cleared up the Basis Theorem proof for you guys. Just to end, here is a little summary of how the Wronskian and Basis theorems help you solve a second order differential equation:

Wronskian tells if you two solutions are linearly independent or not
Basis then allows you to write the complete solution to the homogeneous equation as a linear combination of these two solutions

The Basis Theorem

Like this:

Related

1 Comment

Submit a Comment Cancel reply

Recent Posts

Recent Comments

Archives

Categories

Subscribe to Blog via Email

The Basis Theorem

Share this:

Like this:

Related

1 Comment

Submit a Comment Cancel reply

Recent Posts

Recent Comments

Archives

Categories

Subscribe to Blog via Email