We left the last post on a cliff hanger, namely that in any given metric space, Cauchy sequences need not converge. Now if you’re reading this, you have chosen to take the red pill, and I’m here to show you just how the deep the rabbit hole goes. We shall begin with an example.
Take ![]() with the standard metric
with the standard metric ![]() . Now let us look at the sequence
. Now let us look at the sequence ![]() with
with ![]() . Now we can see that this sequence is Cauchy, the terms get closer and closer together as you increase
. Now we can see that this sequence is Cauchy, the terms get closer and closer together as you increase ![]() . This isn’t obvious at all! So let’s look into this for a bit.
. This isn’t obvious at all! So let’s look into this for a bit.
Clearly, the sequence is never negative, so it is bounded below by zero, this is not the greatest lower bound, the infimum, it is just some lower bound. Now, to show that the sequence get’s closer and closer together with larger values of ![]() , we must show that the sequence is always decreasing, given the special name, monotone decreasing. To do this, we just have to show that
, we must show that the sequence is always decreasing, given the special name, monotone decreasing. To do this, we just have to show that ![]() . So let’s begin.
. So let’s begin.
Proof:
We first consider the difference between two consecutive points in the sequence.
![]()
We need to show that this is greater than zero. We know that ![]() , so we just need to show that
, so we just need to show that ![]() .
.
(1) 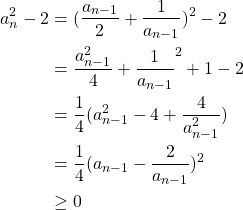
Note this only works for ![]() , i.e. it isn’t true that
, i.e. it isn’t true that ![]() as
as ![]() . And we are done.
. And we are done. ![]() .
.
The sequence is monotone decreasing and bounded below, so in a picture you could imagine all the points getting closer and closer to their greatest lower bound, but still having to decrease, you can imagine that the distance between them will get smaller and smaller by necessity.

Can we prove that this sequence is Cauchy from the definition of Cauchy sequences? I couldn’t, maybe you could though!
Now if this sequence converges to some ![]() then we would have
then we would have
![]()
and therefore we would get ![]() . However,
. However, ![]() , and so the sequence does not converge! Again, another Cauchy sequence that does not converge, except, this time the problem does not lie with the metric we have chosen, instead, the problem is with our metric space, specifically,
, and so the sequence does not converge! Again, another Cauchy sequence that does not converge, except, this time the problem does not lie with the metric we have chosen, instead, the problem is with our metric space, specifically, ![]() does not contain the point
does not contain the point ![]() . It seems the deeper we go down this rabbit hole, the more and more problems we find! So let’s just focus on the things that we like, and we like Cauchy sequences that converge.
. It seems the deeper we go down this rabbit hole, the more and more problems we find! So let’s just focus on the things that we like, and we like Cauchy sequences that converge.
We would like to be able to distinguish between metric spaces in which every Cauchy sequence converges in that space, and the others. A space in which every Cauchy sequence converges in that space is called complete. From our previous example, ![]() is not complete as it did not contain it’s limit point, however, if we had chosen our metric space to be
is not complete as it did not contain it’s limit point, however, if we had chosen our metric space to be ![]() , our sequence would have converged since
, our sequence would have converged since ![]() . In fact, you’d be had pressed to find any Cauchy sequence in
. In fact, you’d be had pressed to find any Cauchy sequence in ![]() that doesn’t converge, that is because,
that doesn’t converge, that is because, ![]() is complete.
is complete.
You may be wandering now, what is ![]() ? After all, if we need to prove something about it, we surely have to know what it is! I won’t construct the real numbers here, rather I will show you what
? After all, if we need to prove something about it, we surely have to know what it is! I won’t construct the real numbers here, rather I will show you what ![]() is and then prove that every Cauchy sequence converges in this place of the “real numbers”.
is and then prove that every Cauchy sequence converges in this place of the “real numbers”.
The real numbers are a set of numbers with addition and multiplication operations which satisfy the field axioms, check out the link for more details on what these are, and there is also a linear order relation ![]() such that
such that
![]()
and that
![]()
However, the most important thing (for us) about the real numbers is that they satisfy the axiom of completeness:
Every non-empty subset that is bounded above has a least upper bound (supremum).
Now we have an idea of what ![]() is, we are in a better position to talk about it. However, as I have done real analysis, this proof that the reals is complete is easiest when we use two known theorems, namely the Bolzano Weirestrass Theorem (every bounded sequence has a convergent subsequence) and the theorem that a Cauchy sequence is bounded. If you don’t know these, look them up! However, assuming you known them, we will jump right into the proof that
is, we are in a better position to talk about it. However, as I have done real analysis, this proof that the reals is complete is easiest when we use two known theorems, namely the Bolzano Weirestrass Theorem (every bounded sequence has a convergent subsequence) and the theorem that a Cauchy sequence is bounded. If you don’t know these, look them up! However, assuming you known them, we will jump right into the proof that ![]() is complete.
is complete.
Proof:
We want to show that any Cauchy sequence converges in ![]() , so let’s begin with the Cauchy sequence
, so let’s begin with the Cauchy sequence ![]() . So for all
. So for all ![]() , there exists an
, there exists an ![]() such that if
such that if ![]() then
then ![]() .
.
Since ![]() is Cauchy, it is bounded, and so by the Bolzano Weirestrass theorem, it has a convergent subsequence
is Cauchy, it is bounded, and so by the Bolzano Weirestrass theorem, it has a convergent subsequence ![]() . So for all
. So for all ![]() , there exists an
, there exists an ![]() such that if
such that if ![]() then
then ![]() . Take
. Take ![]() which forces
which forces ![]() and we get that
and we get that ![]() and
and ![]() . So now we get:
. So now we get:
![]()
.
Hence, all Cauchy sequences converge in ![]() and we are done.
and we are done. ![]() .
.
This idea of complete metric spaces will be very important down in 2 posts time. For now, we look at what is called, a normed vector space, which is the next thing which we will encounter on our voyage through space(s)!

What would we be without the axiom of completeness? Just a couple of hairless apes I’d say. This is the beauty of the human mind. Fantastic post!