Principles: Baire’s Lemma

by | Aug 13, 2020 | Pure Maths | 1 comment

So today I am starting a new series on the Principles of Functional Analysis to give you all an appreciation for the power that these simple truths hold. We will start today with Baire’s Lemma , which will require some definitions, hopefully, all familiar. (If you are not familiar, it’s okay, I’m going to tell you in 3, 2, 1…)

Definition 1 (Dense Set) For a topological space {M}, {A\subset M} is dense if {\bar{A}=M}.

A key example from Real Analysis hours is {\mathbb{Q}} is dense in {\mathbb{R}}. Opposed to the dense set, is the illustrious

Definition 2 (Nowhere Dense Set) For a topological space {M}, {A\subset M} is nowhere dense if {\bar{A}^{\circ}=\emptyset}.

Now that we have these, to get used to the definitions, try proving the following.

Proposition 3 Let {A\subset M}. Then the following are equivalent:

  1. A is open and dense
  2. {A^c} is closed and nowhere dense

Hopefully you’re now cozy with those definitions. It’s time for the main event of this post.

Theorem 4 (Baire) Let {(M,d)} be a complete metric space. Then the countable intersection of open dense sets is dense.

As a first example, if {M} is not complete the conclusion fails to hold. Consider the set {\mathbb{Q}\backslash \{x\}} for any {x\in \mathbb{Q}} and note that these sets are open and dense in {\mathbb{Q}}. However, their intersection is the empty set which is not dense. We can show the following useful equivalence in any metric space, not just a complete metric space.

Lemma 5 Let {(M,d)} be a metric space. The following are equivalent:

  1. the countable intersection of open dense sets is dense
  2. if {M=\cup_{n\in\mathbb{N}}A_n} where each {A_n} is closed, then there exists an {n_0\in\mathbb{N}} such that {A_{n_0}^{\circ}\neq\emptyset}.

Proof: {(1\implies 2)} Suppose that {M=\cup_{n\in\mathbb{N}}A_n} where each {A_n} is closed with empty interior. Then it follows that

\displaystyle \emptyset = \bigcap_{n\in\mathbb{N}}(M\backslash A_n).

However, since each {A_n} is closed and nowhere dense, it follows that {M\backslash A_n} is open and dense and so their countable intersection must be too. A contradiction. {(2\implies 1)} Let {\{A_n\}_{n\in\mathbb{N}}} be a collection of open and dense sets and suppose that there exists an open ball {B:=B_r(x)} such that

\displaystyle B\cap \bigcap_{n\in\mathbb{N}}A_n=\emptyset.

(This is just the definition of the intersection being not dense). It then follows that

\displaystyle M=B^c\cup \bigcup_{n\in\mathbb{N}}A_n^c,

and so it must follow that

\displaystyle (\bigcup_{n\in\mathbb{N}}A_n^c)^{\circ}\neq\emptyset.

Now, the big question is, how do we use (2), to show that one of the sets {A_n^c} has non-empty interior (hence the contradiction)? Well, we just choose a ball that satisfies {B_r(x)\subset \cup_{n\in\mathbb{N}}A_n^c)} and consider the space {(B_r(x),d)} and then apply (2) using the sets {B_r(x)\cap A_n^c}. This gives the existence of an {n_0} such that {B_r(x)\cap A_n^c} has non-empty interior which implies that {A_n^c} has non-empty interior. A contradiction. \Box

This is extremely important, as most of the time, Baire’s lemma is used in the following way. Suppose a complete metric space {M} can be written as the countable union of closed sets, then one of those sets must have non-empty interior. We will see it used in this way in the next post on the uniform boundedness theorem.

I need to mention some terminology. This is where the term Baire Category Theorem comes from. In a metric space {M}, a set is called meagre if it is the countable union of closed, nowhere dense sets. Go back through the previous proof and see if you can spot the meager set. Meagre sets are also said to be of first category. If a set is not of first category it is of second category, also called fat sets (I prefer the term thicc). Finally, a set whose complement is of first category is called co-meagre or residual.

Beware, although these categories mentioned above are mutually exclusive, the same cannot be said about denseness and meagreness. For example try and find a set {A\subset\mathbb{R}} such that {A} is meagre and dense (This should be easy!). For an even more involved example, you could try and show that the C^1([0,1]) functions form a first category set as a subset of C^0([0,1]). (First show that a subset of a meagre set is meagre, then work with Lipschitz continuous functions).

Now, meagerness and fatness (thiccness, for those who have opted for my proposed change in convention), are both measures of how ‘small’ or ‘big’ a set is. But it is not the conventional notion of small or big that you are used to from measure theory. However, we can draw some parallels between these ideas. Namely, a first category set can be thought of as null sets while second category sets as those of positive measure. Keeping with the analogy, the residual sets would be compared to sets that are of full measure. However, these are not exactly the same ideas, to get your head around this, try searching for the following examples.

  1. A meagre set 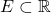{E\subset \mathbb{R}} that has complement with Lebesgue measure zero.
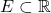  2. A set E\subset\mathbb{R} that is nowhere dense but has infinite Lebesgue measure.

I’m out of time for today, post in the comments your thoughts on the questions above and stay tuned for the problem of the week.

(So from now on, every Thursday night will be a new content post, and on Sunday nights I will post a problem and solve the problem of the previous Sunday)!

1 Comment

  1. Ivan
    Ivan on September 3, 2020 at 3:34 pm

    Great stuff as always Anthony! What is the meaning of the notation A^{\circ}?

    Reply

Submit a Comment

Your email address will not be published.

%d bloggers like this: