On the definition of a Topological Manifold

by | Dec 6, 2018 | Pure Maths | 0 comments

EDIT 7/1/2019: The proof for each finite subset of a Hausdorff space is closed is corrected.

Before I begin, as stated in my articles section, I said I am going to start writing about all the neat maths I’ve learnt throughout my final year project in physics, in which I wrote an introduction to general relativity, (available on the articles page). I’d like to point to a great post written by friend, Ivan, on general relativity. You can find the post here along with all of his other great content.

For those first learning differential geometry, you may be given the definition of a manifold, without any reasoning why the definition is the way it is. We begin with the definition of a topological manifold, if you are unfamiliar with the definition of a topological space, look !!!!here.

A topological manifold is a topological space X such that

  • X is Hausdorff
  • X is second countable
  • X is locally euclidean

A Hausdorff space is a topological space X such that for any two distinct points x,y in X, we can find two open sets U_x and U_y where x\in U_x and y\in U_y and U_x \cap U_y=\emptyset.

Furthermore, a topological space X is called \textit{second countable} if there exists a countable basis for the topology. So this means there exists a countable collection of open subsets of X, U, such that each open subset of X can be written as a collection of elements of some subfamily of U.

Additionally, a topology X is known as locally euclidean if every point in X has a neighbourhood that is homeomorphic to some open subset of \mathbb{R}^n.

We can see automatically why the locally Euclidean condition useful, once we can say that a space is locally like Euclidean space, many of the properties that Euclidean space enjoys are transferred to our topological manifold in a local sense, not necessarily globally. However, the other two conditions, the Hausdorff requirement and the second countability requirement are not so obvious. To see why need the Hausdorff requirement, lets look at what is called the trivial topology, where a topological space X has the topology \{X,\emptyset\}.

We often like to know what a sequence converges to, and so we will first look at how sequences behave in this topology. The first observation we make is that for any sequence in X, it will converge to every point in X. Take (s_n)_{n=1}^{\infty} a sequence in X and some point s\in X. Now in order for s_n \to s, we need for every open neighbourhood of s, there must be points of the sequence also contained in that neighbourhood. Since the only open neighbourhood of s is X, it follows that s_n \to s. But we chose s to be any point in X and so the sequence converges to every point in X.

The next thing that the map F:Y\to X is always continuous for any topological space Y. To check continuity, we look at the pre-images of the open sets of X. Clearly, F^{-1}(\emptyset)=\emptyset and so is open. Now, F^{-1}(X)=Y and so is also open, and hence F is continuous.

This rather pathological example of a topology illustrates the unwanted behaviours that a space can produce itself. Note, that the behaviours had nothing to do with the sequences or the functions we chose, but was a direct consequence of the discrete topology we had chosen. To avoid all this, we restrict ourselves to Hausdorff spaces, and we will now show two important properties of Hausdorff spaces that solve these problems.

For a topological space X that is Hausdorff, each convergent sequence in X has a unique limit.

Proof.
Take a sequence (s_n) in X, and say it converges to two different points s and s'. Since s_n \to s, there exists an N\in\mathbb{N} such that for every open neighbourhood U of s, s_n \in U for all n\geq N. By the Hausdorff property, since s\neq s' there exists an open set V that contains s' and is disjoint to U. Hence s_n \notin V for all n\geq N, and so s_n does not converge to s'. A contradiction and hence s=s' and the limit is unique.
\blacksquare

In order to solve the continuity problem our spaces need sufficient amounts of open sets in order for the definition of continuity to be useful. Now a good way to ensure this is by taking finite subsets to be closed, and so their complements will be open. Since we can construct a vast number of finite subsets, we will also have a vast number of open sets. We now show that each finite subset of a Hausdorff space X is closed.

Proof.
We use the fact if a set contains it’s limit points then it is closed.
Take A\subset X to be finite, and a sequence (s_n) \in A such that s_n\to s for some s\in X. Say that s\notin A, and take some s_n, where n\geq N from the definition of convergence. There is some set V\ni s disjoint from A\ni s_n by the Hausdorff property. However, since s_n \in A for all n, there is an open set V that contains s but does not contain any points of the sequence. A contradiction. Hence, s\in A and A contains it’s limit points.
\blacksquare

EDIT:
This proof is wrong for a few reasons:

  • We didn’t use the fact that the subset is finite anywhere in the proof, other then in the first line where we say it is finite – but this is not used later and so the argument still works for any subset. So our argument states that any subset of a Hausdorff space is closed
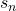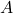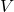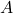  • The second error is that we have misused the Hausdorff property. The property states that given two distinct points, we can find two disjoint sets containing each point. What we have done in the proof is taken a point s_n and a set containing it A, then said we can find a set V containing s that is disjoint to A. This is not the Hausdorff property, and so ultimately the argument breaks down here.

So, a revised proof follows the idea that since the set is finite, A=\{x_1,\dots,\x_N\}, we can write

    \[A=\bigcup \{x_n\},\]

and since each \{x_n\} is a closed set, their finite union is closed. Well, the fact that one point is a closed set is not so obvious, so let’s prove it, and this where the Hausdorff property comes in.

Proof.
Take y\neq x and by the Hausdorff property, we can find two disjoint open sets U_y and U_x such that y\in U_y and x\in U_x. Now, we note that

    \[X\backslash\{x\}=\bigcup_{y\inX,~y\neq x} U_y.\]

Since each U_y is open their union is open and so X\backslash\{x\} is open, and hence \{x\} is closed.
\blacksquare

END EDIT

Now we can see why we need the Hausdorff property in the definition. The second countable condition is to ensure the existence of partitions of unity, I will talk about this in detail in some later post, however, for now, you can think of a partition of unity as way to “glue” different functions on a manifold together. These are required for integrating on the manifold and come up frequently in smooth manifold theory.

Submit a Comment

Your email address will not be published.

%d bloggers like this: